In numerical analysis this method is also know as Newton-Raphson Method named after Isaac Newton and Joseph RaphsonThis method is used for finding successively better approximations to the roots or zeroes of a real-valued function. This post explores the how Newtons Method works for finding roots of equations and walks through several examples with SymPy to.

The Above Expression Must Be Iterated To Obtain The Chegg Com

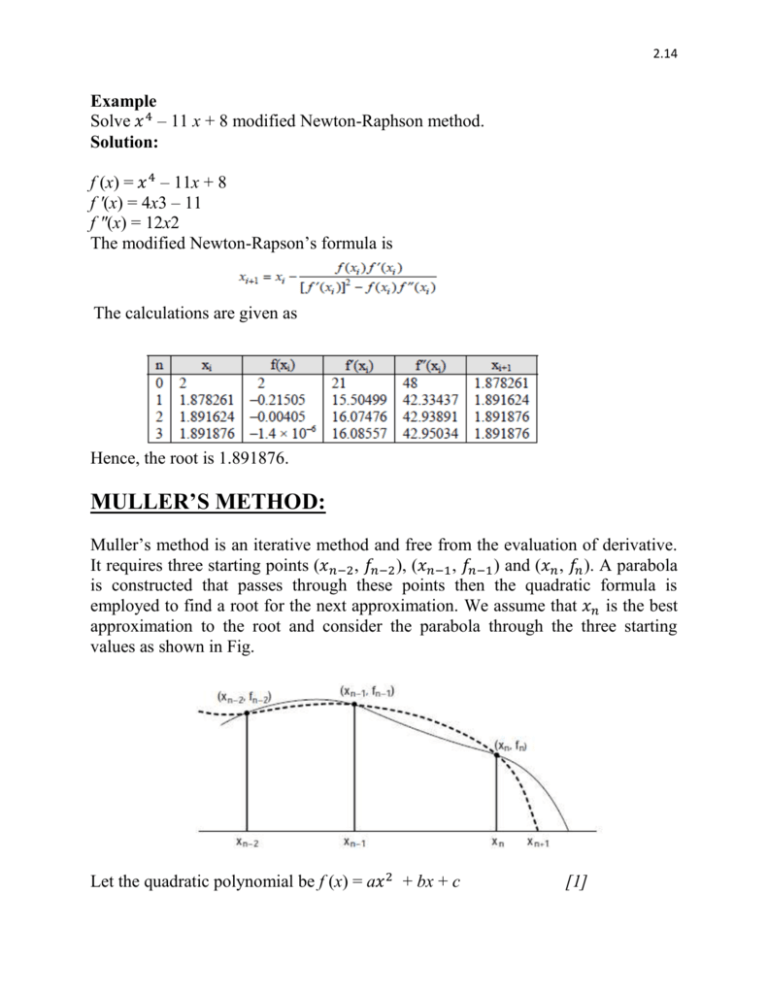
7 Modified Newton Raphson Method
Newton Raphson Method For Solving Non Linear Equations In Matlab Mfile Matlab Programming
Newtons method also known as Newton-Raphson is an approach for finding the roots of nonlinear equations and is one of the most common root-finding algorithms due to its relative simplicity and speed.

Newton raphson method example. Replace the function and its derivative by the one you want to investigate. The root of a function is the point at which fx 0. Python example code for the Newton-Raphson method.
Newton Raphson Method is said to have quadratic convergence. As in the previous discussions we consider a single root x r of the function fxThe Newton-Raphson method begins with an initial estimate of the root denoted x 0 x r and uses the tangent of fx at x 0 to improve on the estimate of the root. The Newton-Raphson method also known as Newtons method is a way to quickly find a good approximation for the root of a real-valued function f x 0 fx 0 f x 0It uses the idea that a continuous and differentiable function can be approximated by a straight line tangent to it.
We make an initial guess for the root we are trying to find and we call this initial guess x 0. Newtons method also known as Newton-Raphson method is a root-finding algorithm that produces successively better approximations of the roots of a real-valued function. 35 minutes Coding time.
Use the Newton-Raphson method to solve a nonlinear equation and 4. Newtons Method also known as Newton-Raphson method named after Isaac Newton and Joseph Raphson is a popular iterative method to find a good approximation for the root of a real-valued function fx 0. Table 1 shows the iterated values of the root of the equation.
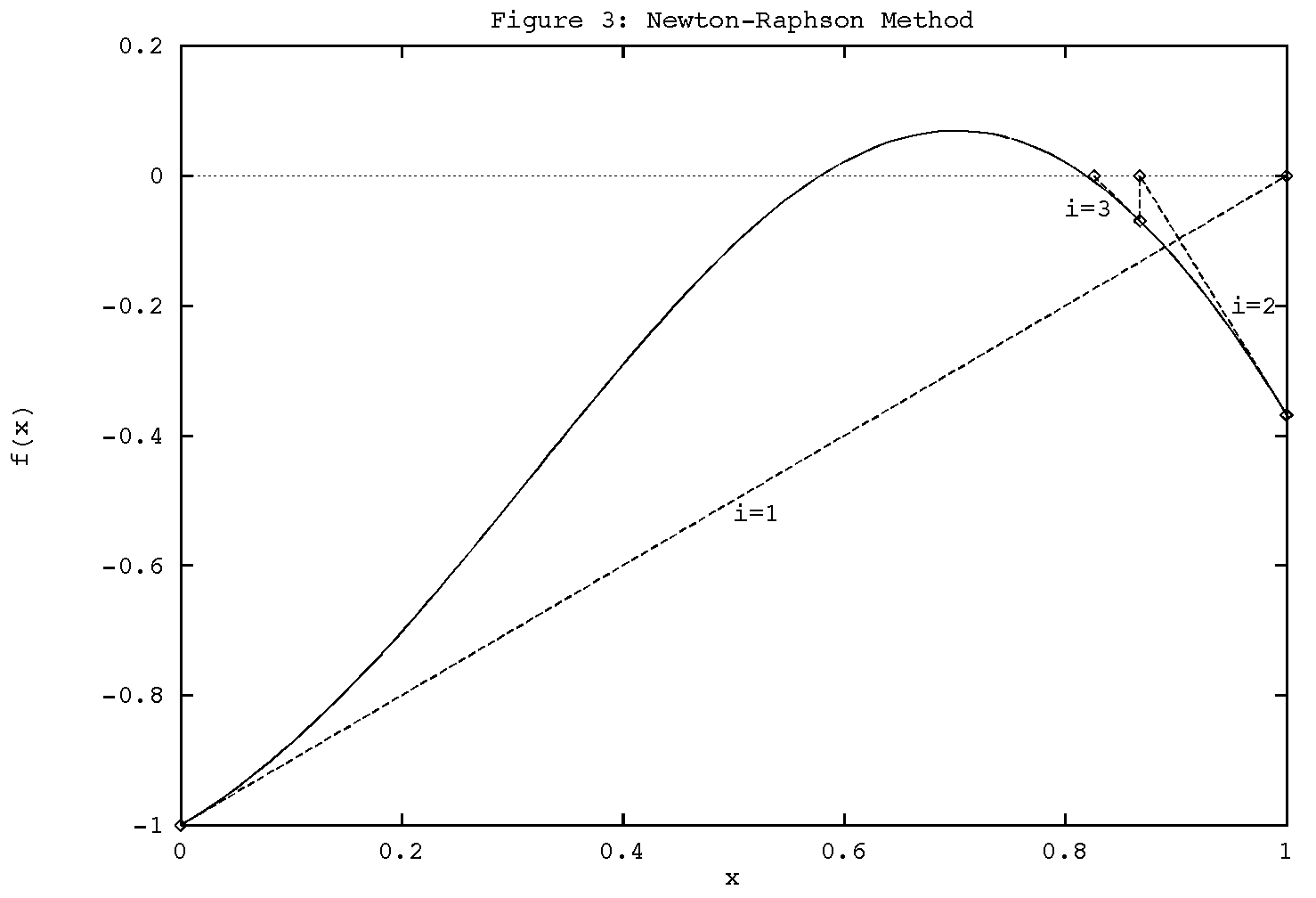
03041 Chapter 0304 Newton-Raphson Method of Solving a Nonlinear Equation After reading this chapter you should be able to. In this section finally I post a short code snippet in python 3 for computing an approximation to a root of a function numerically with the Newton-Raphson method. The root starts to diverge at Iteration 6 because the previous estimate.
Discuss the drawbacks of the Newton-Raphson method. Develop the algorithm of the Newton-Raphson method 3. The Initial Guess Up.
In calculus Newtons method also known as Newton Raphson method is a root-finding algorithm that provides a more accurate approximation to the root or zero of a real-valued function. Reviews 2 Discussions 0 In numerical analysis Newtons method also known as the NewtonRaphson method named after Isaac Newton and Joseph Raphson is a root-finding algorithm which produces successively better approximations to the roots or zeroes of a real-valued function. Like so much of the di erential calculus it is based on the simple idea of linear approximation.
Its required to solve that equation. In numerical analysis Newtons method also known as the NewtonRaphson method named after Isaac Newton and Joseph Raphson is a root-finding algorithm which produces successively better approximations to the roots or zeroes of a real-valued functionThe most basic version starts with a single-variable function f defined for a real variable x the functions derivative f and an. Generated in the manner described below should con-verge to the exact root.
Also it can identify repeated roots since it does not look for changes in the sign of fx explicitly. Also depending on the behavior of the function derivative between x_0 and x_r the Newton-Raphson method may converge to a different root than x_r. The sequence x 0x 1x 2x 3.
Derive the Newton-Raphson method formula 2. Now people have posted examples of where Newtons method doesnt converge but theyre all rather unusual functions some being very non-smooth so its natural to assume theyre pathological and wont happen in practice. Diverging away from the root in ther NewtonRaphson method-For example to find the root of the equation.
Newton Raphson method Algorithm Example-1 fxx3-x-1 online We use cookies to improve your experience on our site and to show you relevant advertising. The Method of False Newton-Raphson Technique The Newton-Raphson method is one of the most widely used methods for root finding. Newton Raphson method with example.
It can be easily generalized to the problem of finding solutions of a system of non-linear equations which is referred to as Newtons technique. The methods discussed above for solving a 1-D equation can be generalized for solving an N-D multivariate equation system. Solution of Non-Linear Previous.
Solving Non-Linear Equations Previous. Newtons method involves choosing an initial guess x 0 and then through an iterative process nding a sequence of numbers x 0 x 1 x 2 x 3 1 that converge to a solution. Fx x3 - 0165x2 399310-4 using Newton-Raphson Method with initial guess x0 005 to 3 iterations and also plot that function.
The approximations of the root go as. The Newton-Raphson method or more commonly Newtons method 3. In particular the improvement denoted x 1 is obtained from determining where the line tangent to fx at x 0 crosses the x-axis.
The Newton Method properly used usually homes in on a root with devastating e ciency. The Newton-Raphson Method 1 Introduction The Newton-Raphson method or Newton Method is a powerful technique for solving equations numerically. 01 Newton Raphson Method The Newton Raphson method is for solving equations of the form fx 0.
It uses the idea that a continuous and differentiable function can be approximated by a straight line tangent to it. Newton-Raphson method univariate Newton-Raphson method multivariate Before discussing how to solve a multivariate systems it is helpful to review the Taylor series expansion of an N-D function. It is worth stating few comments on this approach as it is a more general approach covering most of the iteration schemes discussed earlier.
Newtons method is based on tangent lines. Introduction This article is about Newtons Method which is used for finding roots. Your example is one where Newton just takes more iterations than expected to converge so its not too bad.
For example if the derivative at a guess is close to 0 then the Newton step will be very large and probably lead far away from the root. Alternatively one can also prove the quadratic convergence of Newton-Raphson method based on the fixed - point theory. In calculus Newtons method is an iterative method for finding the roots of a differentiable function F which are solutions to the equation F x 0As such Newtons method can be applied to the derivative f of a twice-differentiable function f to find the roots of the derivative solutions to f x 0 also known as the critical points of f.
C Program for Newton Raphson NR Method with Output Table of Contents. The Newton-Raphson method reduces to. This program implements Newton Raphson method for finding real root of nonlinear equation in C programming language.
For many problems Newton Raphson method converges faster than the above two methods. Starting from initial guess x 1 the Newton Raphson method uses below formula to find next value of x ie x n1 from previous value x n. X_n1 x_n - fx_n fx_n.

Newton Raphson Method Brilliant Math Science Wiki

Newton Raphson The Newton Raphson Method Then Chegg Com
Approximate Solution To An Equation Newton S Method Or The Newton Raphson Method Use Of Newton S Method Example
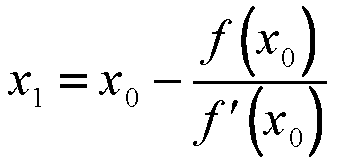
Newton Raphson Technique

Newton Raphson Method Of Solving A Nonlinear Equation More

Chapter 03 04 Newton Raphson Method Of Solving A Nonlinear More Examples Equation
Newton Raphson Technique
X Studygig


